|
|
|
|
|
|
|
|
|
Multiplying and Dividing with Place Value Materials
|
|
|
|
| Place value materials are useful for developing multiplication and division skills only in a limited way - for multiplying by 1-digit numbers and for dividing by 1-digit numbers. For more complex situations the materials tend to confuse the matter rather than assist in developing it. |
|
| Using PV materials for multiplying by 1-digit numbers
Consider 3 x 48. This can be viewed as adding 48 three times.
|
|
|
| Step 1: Build 48 three times |
|
 |
 |
 |
 |
|
|
 |
 |
 |
 |
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
 |
 |
 |
|
 |
 |
 |
|
|
|
 |
 |
 |
 |
|
|
|
|
|
 |
 |
 |
 |
 |
|
 |
 |
 |
|
|
|
| Step 2: Trade |
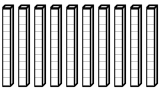 |
 |
|
|
 |
|
|
 |
|
 |
|
|
 |
|
 |
|
 |
|
 |
|
| Step 3: Combine traded and remaining PV materials |
|
|
|
 |
 |
 |
|
 |
 |
|
|
|
|
PV Materials represent answer:
3 x 48 = 144
|
|
 |
 |
 |
 |
|
|
|
|
| Traded PV materials |
Remaining PV materials |
|
|
|
|
|
|
|
Using PV materials for dividing by 1-digit numbers
Consider 65 ÷ 5. This can be viewed as forming five equal groups.
|
|
|
| Step 1: Build 65 |
|
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
| It is not possible to form 5 equal groups of tens. Trading is needed (1 ten for 10 ones). |
|
| Step 2: Trade 1 ten for 10 ones |
|
 |
|
|
|
 |
|
|
|
|
|
 |
|
|
The trading results in 5 tens and 15 ones.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Step 3: Form 5 equal groups. |
 |
 |
 |
 |
 |
|
|
|
 |
 |
 |
 |
 |
|
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
The answer is represented by one of the equal groups.
65 ÷ 5 = 13
|
|
|
|
|
| For more detail, refer to: |
|
|
|
Grade 4 Multiplication Algorithm
Grade 4 Division Algorithm
|
|
|
 |
|
 |
|
|
|
|
|
 |
|
3 x 234 |
|
|
|
|
|
Try these. |
 |
|
|
 |
268 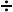 2 2 |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|