|
|
|
 |
|
|
|
A 3-D object can be analyzed with respect to its 0-D, 1-D, and 2-D components. You may be perplexed by the idea of 0-D. A mathematical point is an example of a geometric object that has zero dimensions, because a mathematical point (unlike a point made by a pencil) has no length, no width, and no height/depth.
Consider a cube (look at a real one and examine its features):
|
|
|
 |
|
|
|
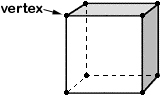
What are the 0-D components of the cube? In other words, what points are essential parts of a cube? There are 8 points that are essential parts, the 8 corners. Each such point is called a vertex. ("vertices" is the plural form) |
|
 |
|
|
 |
|
|
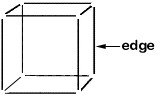
| What are the 1-D components of the cube? In other words, what line segments help define a cube? There are 12 line segments that form the skeleton of a cube. These line segments are called edges. |
|
|
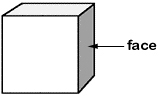
| What are the 2-D components of the cube? In other words, what flat surfaces (parts of planes) help define a cube? There are six flat surfaces that are the skin of a cube. Each flat surface is called a face. |
|
 |
|
|
For more detail on faces, edges, and vertices, refer to Internet resources. |
|
|
|
|
|
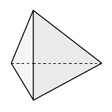
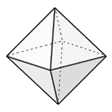
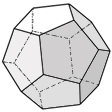
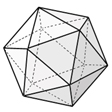
Each object below is one of the five Platonic solids (the cube is the fifth Platonic solid). The five Platonic solids are the only regular convex polyhedra (3-D shapes having no curved surfaces) that are possible. 'Regular' means having equal parts. For example, a cube has 6 faces that are squares.
These Platonic solids turn up in unexpected places. For example, certain viruses have shapes like tetrahedrons, dodecahedrons, and icosahedrons.
Determine the number of faces, edges, and vertices of each '3-D' object (polyhedron) pictured below.
|
|
|
|
|
|
 |
|
 |
|
|
|
|
tetrahedron |
|
|
|
 |
|
 |
|
|
|
|
octahedron |
|
|
|
 |
|
|
|
 |
|
 |
|
|
|
|
dodecahedron |
|
|
|
 |
 |
|
|
|
icosahedron |
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|