Research Interests
My research interests fall into two categories:
Applying computational models of memory and semantics to categorizing and comparing text.
Developing tools to calculate signal detection metrics when the assumptions of the theory of signal detection are violated.
Computational Models of Semantics
Computational models of semantics have enjoyed a good deal of success in modeling human performance over a broad range of cognitive tasks. I apply these models to large corpora of text that are representative of different groups of people to make predictions about how such groups come to have different understandings of the same words. For example, in Aujla (2021), model-generated representations of words from left- and right-leaning news sources successfully predict semantic priming in individuals that identify as readers of the matching news sources.
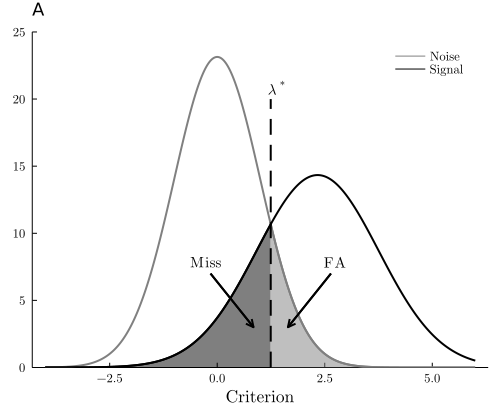
Signal Detection Theory
Signal detection theory (SDT) has been a mainstay in the perception and memory literature for over 50 years. SDT suggests when observers are tasked with making a decision between targets and non-targets, they represent these categories as Gaussian distributions with differing means along an "evidence" axis. Each observer sets a threshold along this axis that determines which stimuli drawn from those distributions is classified as a target or a non-target. In the case of binormal distributions of equal variance with equal numbers of targets and non-targets, the distance between the means of the distributions corresponds to the z-transformed hit rate and false alarm rate scores, called d', irrespective of the observer's decision criterion. However, if this assumption is violated, d' varies depending on the observer's criterion and, therefore, no longer reflects the distance between the means of the distributions. In Aujla (2022), I develop an approach to calculating d' in a way that is consistent across criteria in scenarios where the distributional and base rate assumptions of SDT are violated.
