Tensor Calculus
Partial Derivative of a Tensor
Partial differentiation of a tensor is in general not a tensor. Depending on the circumstance, we will represent the partial derivative of a tensor in the following way
(3.1)
where we have
taken the special case of a contravariant vector .
We now show explicitly that the partial derivative of a contravariant vector cannot be a tensor. Consider the transformation relation for such a tensor.
|
(3.2) |
|
|
Differentiating
with respect to coordinate ,
we find
|
(3.3) |
|
|
Using the chain rule this becomes:
|
(3.4) |
|
|
Expanding this out we get:
If
only the first term on the right-hand side were present, then this would be the
usual tensor transformation law for a tensor of type (1,1). However, the presence of the second term
prevents from behaving like a tensor.
This
problem arises because of the very definition of the derivative. Differentiation involves
comparing a quantity evaluated at two neighbouring points, P
and Q say, dividing by some parameter representing the separation
of P and Q, and then taking the limit as
this parameter goes to zero. In the
case of a contravariant vector field ,
this would involve computing
|
(3.6) |
|
|
for some
appropriate parameter . However, from the transformation law
in the form ,
|
(3.7) |
|
|
we see that
|
(3.8) |
|
|
and
|
(3.9) |
|
|
This
involves the transformation matrix evaluated at different points! Thus
it is clear that is not a tensor. Similar remarks hold for general rank tensor
differentiation.
To define a tensor derivative we shall introduce a quantity called an affine connection and use it to define covariant differentiation. We will then introduce a tensor called a metric and from it build a special affine connection, called the metric connection, and again we will define covariant differentiation but relative to this specific connection.
The Affine Connection and Covariant Differentiation
Consider
a contravariant vector field evaluated at a point Q, with
coordinates
,
near to a point P, with coordinates
. Then, by Taylor's theorem,
to first
order. If we denote the second term by ,
i.e.
(3.11)
then is not tensorial since it involves
subtracting tensors evaluated at two different points. We are going to define a tensorial
derivative by introducing a vector at Q that in some general
sense is 'parallel' to
at P. Since
is close to
,
we can assume that the parallel vector only differs from
by a small amount, which we denote
.
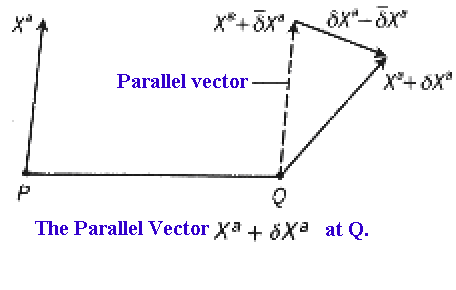
By the same
argument as in previous discussion of the partial derivative, is not tensorial, but we shall construct it
in such a way as to make the difference vector
(3.12)
tensorial. It is natural to require that should vanish whenever
or
does.
Then the simplest definition is to assume that
is linear in both
or
,
which means that there exist multiplicative factors
where
|
|
|
and the minus sign is introduced to agree with convention.
We
have therefore introduced a set of functions
on the manifold, whose transformation
properties have yet to be determined.
This we do by defining the covariant derivative of
,
(usually written in one of the following notations
) by the limiting process
(3.14)
In
other words, it is the difference between the vector and the vector at Q that is
still parallel to
,
divided by the coordinate differences, in the limit as these differences tend
to zero. Using (3.10)
and (3.13),
we find
(3.15)
or in terms of the semi-colon notation
(3.16)
Note
that in the formula the differentiation index comes second in the downstairs indices of
. If we now demand that
is a tensor of type (1,1), then a
straightforward calculation (exercise) reveals that
must transform according to
or equivalently (exercise)
.
If the second term on the right-hand side were absent, then this would be the usual transformation law for a tensor of type (1,2). However, the presence of the second term reveals that the transformation law is linear inhomogeneous. (3.17) or (3.18) is called an affine connection [or sometimes simply a connection or affinity]. A manifold with a continuous connection prescribed on it is called an affine manifold. From another point of view, the existence of the inhomogeneous term in the transformation law is not surprising if we are to define a tensorial derivative, since its role is to compensate for the second term that occurs in (3.5).
We next define the covariant derivative of a scalar field to be the same as its partial derivative, i.e.
|
(3.19) |
|
|
If we now demand that covariant differentiation satisfies the usual product rule of calculus, then we find
(3.20)
Notice
again that the differentiation index comes last in the -term and that this term enters with a minus
sign. The name covariant derivative
stems from the fact that the derivative of a tensor of type (p, q) is of type
(p, q+1), i.e. it has one extra covariant rank. The expression in the case of a general tensor is:
(3.21)
It
follows directly from the transformation laws that the sum of two connections
is not a connection or a tensor.
However, the difference of two connections is a tensor of type
(1,2), because the inhomogeneous term cancels out in the transformation. For the same reason, the anti-symmetric part
of a ,
namely,
|
(3.22) |
|
|
is a tensor (called the torsion tensor). If the torsion tensor vanishes, then the connection is symmetric, i.e.
|
(3.23) |
|
|
Affine Geodesics
If
is any tensor, then we introduce the notation
|
(3.24) |
|
|
that is, of a tensor is its covariant derivative
contracted with
. A
contravariant vector field
determines a local congruence of curves,
whenever the tangent vector field to the congruence is
We next define the
absolute derivative of a tensor along a curve C of this
congruence,
written ,
by the following relation
|
|
|
The
tensor is said to be parallely
propagated, or parallel transported, along the curve C
if
|
|
|
This is a
first-order ordinary differential equation for ,
and so given an initial value for
,
say
,
equation (3.26)
determines a tensor along C which is everywhere 'parallel' to
.
Using this notation, an affine geodesic is defined as a privileged curve along which the tangent vector is propagated parallel to itself. In other words, the parallely propagated vector at any point of the curve is parallel, that is, proportional to the tangent vector at that point:
|
(3.27) |
|
|
Using (3.25), the equation for an affine geodesic can be written in the form
|
(3.28) |
|
|
or equivalently (exercise)
|
(3.29) |
|
|
The last result is
very important and so we shall establish it afresh from first principles using
the notation of the last section. Let
the neighbouring points P and Q on C
be given by and
|
(3.30) |
|
|
to first order in ,
respectively. This is essentially a
Taylor expansion. We define
|
|
|
The vector at P is now the tangent vector
. The vector at Q parallel to
is, by (3.13)
and(3.31),
|
(3.32) |
|
|
The vector already at Q is
|
(3.33) |
|
|
to first order in . These last two vectors must be parallel, so
we require
(3.34)
where we have
written the proportionality factor as without loss of generality, since the
equation must hold in the limit
. Subtracting produces the equation we
obtained before:
|
(3.35) |
|
|
Note that appears in the equation multiplied by the
symmetric quantity
,
and so even if we had not assumed that
was symmetric the equation picks out its
symmetric part only.
If
the curve is parameterized in such a way that vanishes (that is, by the above, so that the
tangent vector is transported into itself), then the parameter is a privileged
parameter called an affine parameter, often conventionally denoted by s,
and the affine geodesic equation reduces to
|
(3.36) |
|
|
or equivalently
|
(3.37) |
|
|
An affine parameter s is only defined up to an affine transformation (exercise)
|
(3.38) |
|
|
where and
are constants. We can use the affine parameter s to define the affine
length of the geodesic between two points
and
by
,
and so we can compare lengths on the same geodesic. However, we cannot compare lengths on
different geodesics (without a metric) because of the arbitrariness in the
parameter s. From the existence
and uniqueness theorem for ordinary differential equations, it follows that
corresponding to every direction at a point there is a unique geodesic passing
through the point as shown below.

Similarly, as long as the points are sufficiently 'close', any point can be joined to any other point by a unique geodesic. However, in the large, geodesics may focus, that is, meet again as shown in the following diagram.
