The Spacetime of General Relativity

 

 

Special Relativity as a Spacetime Subclass

 

When the gravitational field is zero, the spacetime of General Relativity is the spacetime of Special Relativity. Special Relativity involves a Riemannian manifold with the property that there exists a global coordinate system in which the metric takes the form

 

 

(10.1)

This metric is called the Minkowski Metric. Such a global coordinate system is called an inertial system or a Cartesian coordinate system. Let  be points in spacetime and let these points be called events. In Special Relativity we may always introduce a Cartesian coordinate system about any point so that

 

(10.2)

 

The coordinate neighbourhood in the case of Special Relativity is the entire manifold.

 

The line element in Special Relativity can be written as

 

(10.3)

 

This expression, expanded out, gives the familiar Special Relativity invariant distance in terms of Cartesian coordinates.

 

 

(10.4)

 

 

Let's consider the Special Relativity metric in spherical polar coordinates.

(10.5)

The coordinate transformation is as follows

 

(10.6)

The line element takes the form

 

 

(10.7)    

The metric for the polar coordinate case can be written as follows

 

(10.8)  

The affine connection arising from this metric is not as simple as the zero component Cartesian coordinate case. We have

 

(10.9)

It is not obvious anymore whether the Special Relativity Riemann tensor globally obeys .  However, a direct calculation shows that it is still true.

 

 

Null Cones in Special Relativity

 

 

Consider an arbitrary vector . The magnitude of this vector is given by the following dot product

 

(10.10)

 

 

We classify such vectors according to the value of this dot product according to the following scheme.

 

(10.11)

 

(10.12)

 

(10.13)

 

Two distinct null vectors are always orthogonal to each other. With respect to any point P in special relativity, the set of all null vectors passing through P generates a double cone surface, which is called the light cone. It's defining equation is obtained from (10.13) and in expanded form is written

 

(10.14)  

 

This light cone is shown in the following diagram. All null vectors passing though P must lie on the surface of the up and down cones. All timelike vectors going through P must be inside these cones. All physical processes will trace out causality paths going from the bottom to the top of the diagram.

P

 

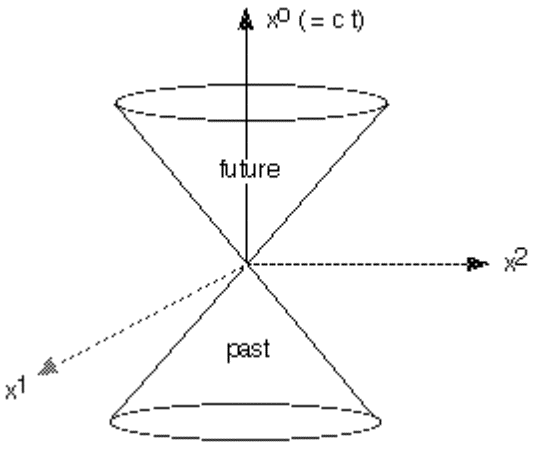
Given a timelike vector  then any null vector or timelike vector  is said to be future pointing if

 

(10.15)

and past pointing if

 

(10.16)

 

 

 

 

The Relationship between the Spacetimes of

General Relativity and Special Relativity

 

For General Relativity we demand that locally the spacetime is the spacetime of Special Relativity. About any point  a coordinate system where       

(10.17)

 

 

As we have seen, we can always use geodesic coordinates about any point P of a GR spacetime to obtain

 

(10.18)

,

 

and without loss of generality arrange this coordinate system such that the origin is situated at point P:

 

(10.19)

.

 

 

 

Since we have now adopted as our affine connection the metric connection given by

(10.20)  

the coordinate equation (10.18) has implications for the metric tensor. We know that the covariant derivative of the metric vanishes and therefore we the following relation holds everywhere.

 

(10.21)  

 

 

 

With geodesic coordinates at P we then must have

 

(10.22)

For points near the point P we can use a Taylor expansion of the metric tensor to get the following:

 

 

(10.23)  

 

A linear transformation

 

(10.24)

(where the  are constants of a nonsingular matrix) can be used to get the metric   into diagonal form with values  as the diagonal entries. We want the matrix to look like

  

so that we will be in correspondence locally with Special Relativity. Due to the linearity of the coordinate transformation the pattern of the previous coordinate equations remains intact at point P:

 

(10.25)

 

and

(10.26)

 

The difference is that now  is a diagonal matrix. The requirement that the spacetime of GR be locally Special Relativity implies that this diagonal matrix is . Therefore we have constructed a coordinate system about P in which, for the neighbourhood of P, the following must hold.

 

(10.27)  

 

 

 

We see from this result that very close to P we will always have

 

(10.28)

 

Notice from (10.27) that the departure from flatness depends on the 2nd order derivative of the metric , which does not vanish at P.