Rotating Black Hole

 

To obtain the vacuum solution for a rotating black hole is a complicated process. It was first done by the New Zealand mathematician Roy Kerr in 1963. There are several forms for the coordinates. We will briefly discuss one version. Since the main symmetry for a rotating spherical object is about its spinning axis the Kerr solution is said to be axisymmetric. The stationary line element in the Cartesian coordinates  that Kerr used is as follows:

 

 

(24.1)

 

where .

 

 There are two parameters here:

 

 

 

The Kerr solution has a singularity at the point  and each of the points lying on the ring of points defined by . This ring lies in the equatorial plane defined by .

 

 

For , there are two event horizons given by the following equations:

 

(24.2)

 

and

 

(24.3)

 

 

 

The boundaries fixed by these event horizons define three regular point regions:

 

 

 

Note that in the limit that ,  

 

 

 

 

 

 

 

 

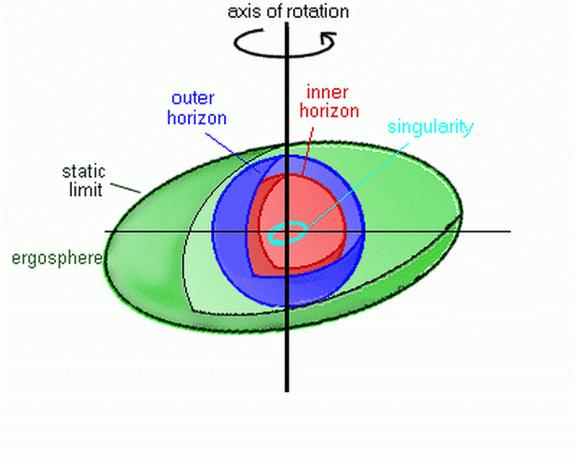
The ergosphere is a region outside of the outer event horizon.

 

 

 

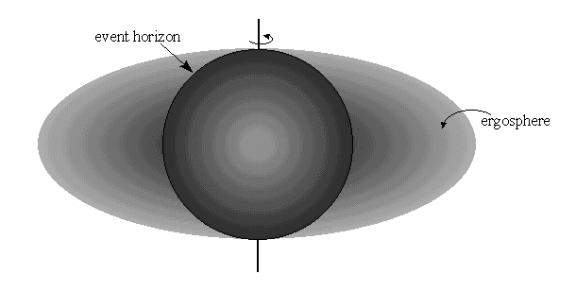
In the ergosphere the rotating Black Hole drags space around with it (called frame dragging) in such a way that all objects inside the ergosphere must rotate with the Black Hole. No time-like curves exist that go in the opposite direction. The static limit is the outer boundary of the ergosphere region since inside the ergosphere a body can never remain in a static position.