Radially Infalling Particles

 

We will now discuss what happens when a particle falls radially inwards towards the spherically symmetric gravitational field source. This means that in spherical coordinates we are insisting that

 

 

(21.1)

 

 

 

We want the particles to be normal test particles with a small mass incapable of changing the overall curvature of the local environment, which is being produced by the large mass m. Since we are considering the situation where no other external forces are present we expect that these particles will travel on timelike equations governed by the geodesic equations.

 

(21.2)

 

This equations gives rise to two differential equations in terms of the proper time :

 

(21.3)

 

 

 

(21.4)  

 

 

Exercise: check this.

 

 

The constant k is determined by the initial conditions. We will choose the initial set up to be that of a particle coming from an infinite distance away from the gravitational source. This particle is set to have zero initial velocity. It can easily be shown that this situation implies

(21.5)

.

 

From the 1st differential equation (21.3) we then see that

 

(21.6)

 

 

 

Hence

 

(21.7)

 

 

With this choice of initial conditions we can now solve the system of two differential equations (21.3) and (21.4) to give the following result.

 

 

 

(21.8)

 

 

For the radially infalling case we must take the negative square root solution of this equation.

 

 

(21.9)

 

 

 

 

 Integrating this equation we arrive at the result:

 

 

(21.10)

 

 

The integration constants  and  are arranged such that

 

 

(21.11)

 

 

 

Notice that this equation does not do anything strange at the Schwarzschild Radius .

 

(21.12)

 

 

The body obviously falls towards the origin in a finite amount of proper time!

 

This finite time calculation is not upheld however if we switch to coordinate time. We will now show this. Consider the relation.

 

 

(21.13)

Using the differential equations for our initial conditions we get the following.

 

 

(21.14)

 

 

Solving this differential equation leads to the equation:

 

 

(21.15) .

 

Note that  is built into this equation. The big difference comes when we look at small values of the radial coordinate. In this limit it can be shown (exercise) that the following result must be true.

 

 

 

(21.16)

 

This implies that when  

 

(21.17)

 

 

The radius  is approached but the observer, who uses the coordinate time at infinity never sees the object cross this value.

 

 

 

The ideas discussed above are illustrated in the following diagram. The particle starts its infalling journey at the top of the diagram.

 

 

 

 

 

 

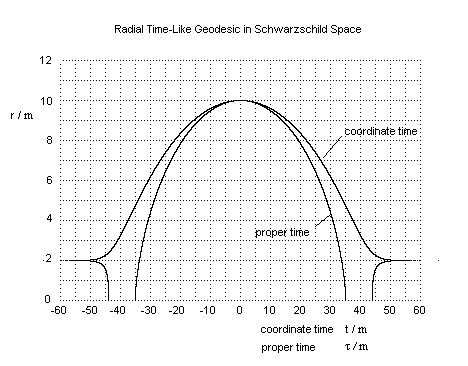
See this page for a good discussion of the infalling case: Click here.