Introduction to the Metric
Metric Fundamentals
Any
symmetric covariant tensor field of rank 2, say ,
defines a metric. A manifold endowed with a metric is called a
Riemannian manifold. A metric can be used to define distances
and lengths of vectors. The
infinitesimal distance (or interval in relativity), which we call
,
between two neighbouring points
and
is defined by
Note
that this gives the square of the infinitesimal distance, .
This is conventionally written as
. The equation (6.1) is
also known as the line element. The square of the length of a contravariant vector
is defined by
|
(6.2) |
|
|
The
metric is said to be positive definite or
negative definite if, for all vectors ,
or
,
respectively. Otherwise, the metric is
called indefinite. The angle between two vectors
and
with
and
is given by
(6.3)
In particular, the vectors and
are said to be orthogonal
if
|
(6.4) |
|
|
If the metric is indefinite (as in relativity theory), then there exist vectors that are orthogonal to themselves called null vectors, i.e.
|
(6.5) |
|
|
The determinant of the metric is denoted by
|
(6.6) |
|
|
The metric is non-singular if ,
in which case the inverse of
,
,
is given by the relation
|
(6.7) |
|
|
It
follows from this definition that gab is a contravariant tensor or rank 2
and it is called the contravariant metric. We may now use and
to lower and raise tensorial indices by
defining
|
(6.8) |
|
|
and
|
(6.9) |
|
|
where we use the
same kernel letter for the tensor.
Since from now on we shall be working with a manifold endowed with a
metric, we shall regard such associated contravariant and covariant tensors as
representations of the same geometric object. Thus, in particular, ,
,
and
may all be thought of as different
representations of the same geometric object, the metric g. Since we can raise and lower indices freely
with the metric, we must be careful about the order in which we write
contravariant and covariant indices.
For example,
could possibly be different from
.
Metric Geodesics
Consider the time
like curve C with parametric equation . Dividing equation (6.1),
which we write as
|
(6.10) |
|
|
by the square of we get
|
|
|
Then the interval s between two points P1 and P2 on C is given by
(6.12)
|
|
|
|
We define a timelike metric geodesic between any two points P1 and P2 as the privileged curve joining them whose interval is stationary under small variations that vanish at the end points. Hence, the interval may be a maximum, a minimum, or a saddle point. Deriving the geodesic equations involves the calculus of variations and the use of the Euler-Lagrange equations. The Euler-Lagrange equations result in the second-order differential equations
(6.13)
|
|
|
|
where the quantities in curly brackets are called the Christoffel symbols of the first kind and are defined in terms of derivatives of the metric by
Multiplying through by and using
we get the equations
|
|
|
|
where are Christoffel
symbols of the second kind defined by
|
|
|
In addition, the
norm of the tangent vector is given by (6.11). If, in particular, we choose a parameter u
which is linearly related to the interval s, that is,
(6.17)
where and
are constants, then the right-hand side of (6.15)
vanishes. In the special case when
,
the equation for a metric geodesic becomes
|
(6.18) |
|
|
and
|
(6.19) |
|
|
where we assume .
Apart from trivial
sign changes, similar results apply for spacelike geodesics, except that we replace s by ,
say, where
|
(6.20) |
|
|
We would have in this case
|
(6.21) |
|
|
and
|
(6.22) |
|
|
where we assume .
However, in the case of an indefinite metric, there exist geodesics, called null geodesics, for which the distance between any two points is zero. It can also be shown that these curves can be parameterized by a special parameter u, called an affine parameter, such that their equation does not possess a right-hand side, that is,
(6.23)
where
|
(6.24) |
|
|
The last equation follows since the distance between any two points is zero, or equivalently the tangent vector is null. Again, any other affine parameter is related to u by the transformation
|
(6.25) |
|
|
where and
are constants.
The Metric Connection
In general, if we have a manifold endowed with both an affine connection and metric, then it possesses two classes of curves, affine geodesics and metric geodesics, which will be different as shown in the diagram below where affine geodesics are in the up/down direction and the metric geodesics are in the right/left direction.
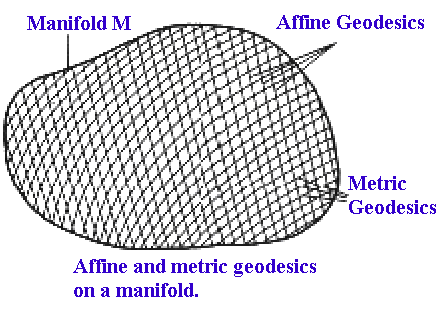
However, comparing the two curve equations (3.37) and (6.17):
we see that the two classes of curves will coincide if we take
|
(6.26) |
|
|
or, using (6.16) and (6.14), if
It follows from the last equation that this special connection based on the metric is necessarily symmetric, i.e.
|
(6.28) |
|
|
If one checks the
transformation properties of from first principles, it does indeed
transform like a connection (exercise).
This special connection built out of the metric and the metric's
derivatives is called the metric connection. From now on, we shall always work
with the metric connection and we shall denote it by
rather than
,
where
is defined by (6.27). This definition leads immediately to the
identity (exercise)
|
|
|
Conversely, if we require that (6.29) holds for an arbitrary symmetric connection, then it can be deduced (exercise) that the connection is necessarily the metric connection. Thus, we have the following important result.
Theorem: If denotes the covariant derivative defined in
terms of the affine connection
,
then the necessary and sufficient condition for the covariant derivative
of the metric to vanish is that the connection is the metric
connection.
In addition, we can show that
|
(6.30) |
|
|
and
|
(6.31) |
|
|