Coordinate Hypersurfaces
We will now discuss the characterization of complicated coordinates. Situations inevitably arise in General Relativity where the 4-D coordinates are so complicated that the standard roles of particular coordinates as time or space variables are obscured.
One of the ways of attacking the problem of sorting things out is to look at hypersurfaces at various points in the manifold. A hypersurface is defined as the surface that arises from fixing a coordinate to be the same value.
(20.1)
Here the superscript (alpha) is meant to convey
the idea that we have picked a specific value for the coordinate: ,
,
,
or
.
We want to classify these hypersurfaces as being timelike,
null, or spacelike.
To get this information we will look at the normal to the hypersurface. The
normal vector is defined as follows:
(20.2)
The diagram below shows hypersurfaces with paths that are normal (F
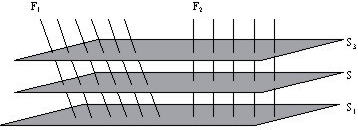
We now establish the contravariant form of the normal.
(20.3)
This leads to the contravariant normal in the following succinct notation form
|
(20.4) |
|
|
This tells us that we can get the contravariant hypersurface normal vector by simply looking at the contravariant metric tensor. Whether the normal is timelike, null, or spacelike is determined by it's 4-magnitude.
|
(20.5) |
|
|
The possibilities are
|
(20.6) |
|
|
We will rewrite this in terms of the metric.
|
(20.7) |
|
|
,
which gives the following
|
(20.8) |
|
|
Note that there is no implied sum here since we are assuming that (alpha) is just some fixed number {0,1,2, or 3}. This relation now gives us an easy way to pick out the timelike, null, or spacelike character of the hypersurface.
|
(20.9) |
|
|
The formalism of general relativity allows for the signature to be arbitrary. However the most common situations for the hypersurface character is as follows:
Consider the Schwarzschild metric in contravariant form
This tells us that the hypersurfaces are organized as follows
A diagram showing constant time hypersurfaces that are timelike is given below.
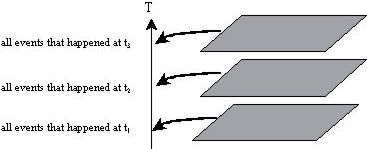
Note that when the roles of the time coordinate t and the
polar coordinate r switch. The contravariant metric (20.10) implies that the
variable t becomes a spacelike coordinate and the variable r becomes a timelike
coordinate. This means that if you have a position coordinate such that
,
then space becomes dynamic. You have to do nothing at all before you will be at
the singularity point
.
Space is being annihilated.