Black Holes
In the Schwarzschild
solution there is always a natural lower limit on the radius coordinate for a
star. For a normal star this lower limit would be .
For a star that has undergone gravitational collapse
,
the Schwarzschild Radius, is the lower
bound (-remember it's
in normal units). After that value the radius
coordinate becomes a timelike variable. If we want to investigate the properties
of the collapsed object, called the Black Hole, we need to get a better set of
coordinates than the Schwarzschild coordinates. A better set is found by
adopting the following new time coordinate.
The line element,
written in terms of proper time ,
can then be calculated to be
(22.2)
These coordinates are called the Eddington-Finkelstein Coordinates.

In these coordinates none of the metric elements becomes infinite at the Schwarzschild Radius.
We should be able to cross over the boundary without problems.
Now consider what
light does as it falls radially inwards on the Black Hole. Using the above line
element we use the radial constraint condition to arrive at the following differential
bifurcation equation for null geodesics (
):
(22.3)
The bifurcation logic implies that we have
(22.4)
with solution
(22.5)
OR
(22.6)
with solution
(22.7)
We will now figure out what these solutions mean physically.
From the equation (22.1) we have the derivative relation
The first bifurcation solution then implies the following
(22.9)
Note that this means
(22.10)
Hence the first bifurcation equation solution must correspond to ingoing null geodesics.
(22.11)
What about the 2nd bifurcation equation? From equation (22.8) we see that
(22.12)
Note that this means
(22.13)
Hence the second bifurcation equation solution must correspond to outgoing null geodesics.
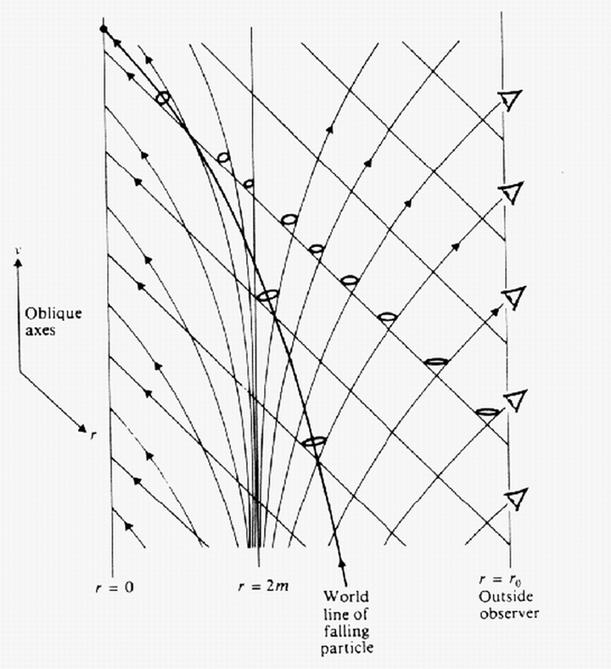
The diagram below show a v versus r diagram with representative null
geodesics going in towards the black hole and going away from the black hole.
The v-r axes are drawn as oblique axes. The ingoing null geodesics, , are parallel to the r axis, a line drawn
to the vertical. They extend down to the mass
source, situated at
.
The outgoing null geodesics asymptotically coincide
with the value
when
.
A photon starting on
the outside of the black hole will travel through the Schwarzschild Radius. A
photon that starts on the inside of the Schwarzschild Radius, on the other
hand, never has a path that leads outside of the black hole. It is trapped. If
we had a dense collection of mass with a physical surface boundary less than
its Schwarzschild Radius, light from the surface could not escape from it to
the outside .
An outside observer could detect the object's existence through its
gravitational field but that observer would not be able to see it. This is the
reason why such objects came to be known as black holes. The sphere defined by
shouts off the outside world from observing
what's inside. For this reason the region where
is said to constitute the Event Horizon.
The large 3million solar mass black hole called Sagittarius A, situated at the center of the Milky Way Galaxy, is confined to a region no larger than our solar system. It would be quite possible to pass the Schwarzschild Radius boundary of this black hole without anything untoward happening. However, once you were within this boundary, no signals could ever be sent to the outside world. All paths would point to the singularity at the center.
Another set of coordinates that turn out to be very useful in describing the black hole, and actually do a more complete job of doing this than any other set of known coordinates, are called Kruskal Coordinates. In Kruskal coordinates both the r and the t coordinates of the Schwarzschild solution are transformed in a transcendental way as follows.
(22.14)
(22.15)
In terms of proper time, this leads to the line element
(22.16)
Note that this line element has no problems with the Schwarzschild Radius. The variable r in these equations has no status as a coordinate anymore but is defined implicitly by the relation
(22.17)
With these coordinates the radial null geodesics are given by straight lines, not just for the ingoing geodesics, but also for the outgoing geodesics. Their equations are
(22.18)
which are lines that are at to the vertical and horizontal in a u-v
spacetime diagram. This is then very similar to the spacetime diagrams in
Special Relativity.
|
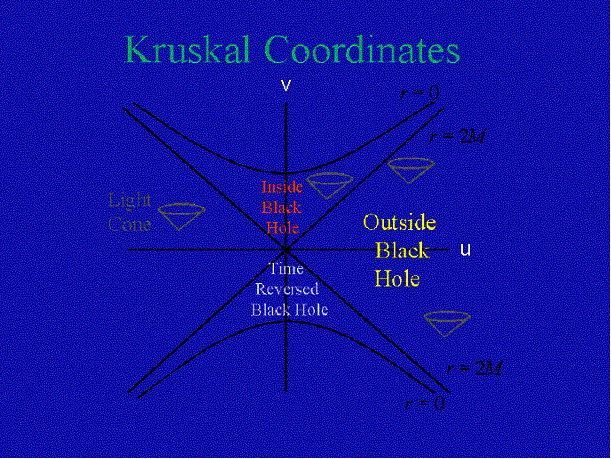
The Kruskal solution
is called the Maximal Extension solution since it takes in regions of the
manifold that are not covered by other coordinate systems. This extended
manifold is represented in the Kruskal diagram shown above. Note that this
solution implies the existence of a parallel universe on the left hand side
of the diagram. There is no causal contact with this universe since all paths
towards it must travel inside the black hole and all inside paths crash into
the singularity at |